La sucesión de Fibonacci es una de las secuencias más conocidas de las matemáticas, una serie de números que guardan una estrecha relación con los anteriores, partiendo del «0» y el «1», y, que se relacionan en gran medida con la proporción áurea, el número de oro y la estética. Existen muchas curiosidades y datos interesantes sobre la sucesión de Fibonacci que repasaremos en este artículo de 10 cosas que quizás no sabías sobre la sucesión de Fibonacci.
¿Qué es la sucesión de Fibonacci?
Antes de comenzar, debemos tener clara la respuesta a la pregunta de qué es la sucesión de Fibonacci. La sucesión de Fibonacci, también conocida como la serie de Fibonacci es una sucesión de números naturales en la que cada término es la suma de los dos términos anteriores. Esta sucesión comienza con los números «0» y «1», y continua de la siguiente manera:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610…
La representación de la sucesión de Fibonacci matemáticamente es:
- f (0)=0
- f (1)=1
- f(n)= f(n-1) + f(n-2)
Infinita
La sucesión de Fibonacci es una sucesión infinita de números naturales que comienza con los números «0» y «1», y, dada su naturaleza, crece exponencialmente sin ningún tipo de límite. Como hemos comentado, cada nuevo término es la suma de los dos términos anteriores, por lo que, dado que los números son infinitos, la sucesión es por consiguiente ilimitada, creciendo cada vez más rápidamente hasta el infinito.
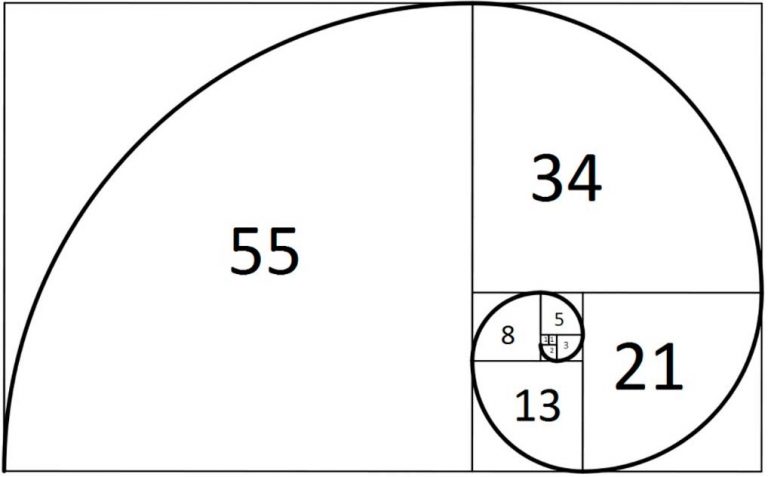
Representación gráfica en espiral
La sucesión de Fibonacci suele representarse gráficamente como una aproximación a la proporción aurea de la espiral dorada, al inscribirse en cuadrados cuyos lados contengan la propio serie de Fibonacci. Esta espiral logarítmica responde a un crecimiento a razón del número áureo, representado con la letra «phi», y, se puede observar en diversos lugares en la naturaleza. No obstante, cabe decir que la sucesión de Fibonacci se aproxima a la proporción áurea, pero, no es exacta.
Explicación Áurea
Indagando más en la razón áurea, cabe señalar que el cociente entre un término de la serie y el anterior varía proporcionalmente, pero, se estabiliza conforme crece la sucesión, aproximándose al número áureo. Explicado de manera numérica:
- 1/1= 1
- 2/1 = 2
- 3/2= 1,5
- 5/3= 1,667
- 8/5= 1,6
- 13/8= 1,625
- 21/13= 1,615
- 34/21= 1,619
- 55/34= 1,618
- 89/55= 1,618
¿Quién fue el autor de la sucesión de Fibonacci?
Leonardo de Pisa, conocido como Fibonacci, fue un matemática italiano que vivió en la República de Pisa durante la Edad Media, entre los años 1170 y 1240. Se trata de uno de los matemáticos más reputados de la historia, difundiendo el sistema de numeración indo-arábigo frente a la numeración romana, y, escribiendo varios libros como «Liber Abaci», la «Práctica Geometriae», o, el «Liber Quadratorum», el libro de los números cuadrados que explica una serie de propiedades de estos números.
Sucesión de Fibonacci en la naturaleza
La sucesión de Fibonacci puede verse en múltiples elementos de la naturaleza. Uno de los ejemplos más claros se observa en la concha de un nautilus, un tipo de molusco cefalópodo marino que dio nombre al submarino más importante de la literatura universal en «Veinte mil leguas de viaje submarino» de Julio Verne.

Sucesión de Fibonacci en el cine
La película del Código Da Vinci de 2006, basada en el libro de Dan Brown del mismo nombre del año 2003, cuenta con numerosos términos matemáticos como la sucesión de Fibonacci, la proporción áurea, el pentáculo, o, la teoría del conteo. A raíz del lanzamiento de la película estos términos se han comenzado a expandir, casi tanto como las espirales de la sucesión de Fibonacci cuando tiende a infinito.
Número áureo
El número áurea, conocido también como el número de Dios, la proporción áurea, la razón áurea o el número de oro es un número irracional infinito cuyo valor es 1,618033988, es decir, aproximadamente el cociente de la división de dos números consecutivos en la sucesión de Fibonacci cuando tiende a infinito. El número áureo es importante ya que se supone la divina proporción, atribuyéndole un carácter estético divino, así como un misticismo único.

Apuestas con la sucesión de Fibonacci
La secuencia matemática de Fibonacci se puede aplicar a diversos ámbitos de la vida cotidiana, utilizándose como base para una estrategia de un sistema de apuestas de casino. El sistema de apuestas de Fibonacci consiste en aumentar la apuesta cada vez que se pierde, y, disminuir la apuesta cuando se gana, buscando ganar mayor dinero en las apuestas que se ganan, y, perder menos dinero en las apuestas que se pierden. Para ello, se utiliza la serie de Fibonacci para marcar la cantidad a apostar en cada ronda, siguiendo los números, lo que equivaldría aproximadamente a multiplicar la apuesta o dividirla por 1,6.
Los conejos de Fibonacci
En el año 1202 Fibonacci propuso un problema para explicar de manera «divertida» y «visual» la sucesión por la que es conocido a día de hoy. Para ello, Fibonacci parte de una pareja de conejos, y, se pregunta cuántas parejas de conejos se pueden obtener, sabiendo que cada pareja tiene al mes una nueva pareja de bebés, la cuál no tendrá nuevos conejos hasta ser adulta al cabo de dos meses.
Por tanto, al principio hay 1 pareja de conejos «bebés», al cabo de un mes sigue habiendo 1 pareja de conejos ya adultos, al cabo de dos meses habrá 2 parejas de conejos, una adulta y otra bebé, al cabo de tres meses habrá 3 parejas de conejos, dos adultas y una bebé, al cabo de cuatro meses habrá 5 parejas de conejos, tres adultas y dos bebés, al cabo de cinco meses habrá 8 parejas de conejos, cinco adultas y tres bebés…Como vemos, este problema guarda la sucesión de Fibonacci.






